【题解】 tower 网络流 bzoj4657 | Qiuly's blog!

【题解】 tower 网络流 bzoj4657

Posted on | Edited on | In | Comments:

考试的时候正好考了这道题，全场仅有 $lys$ 大佬 $AC$ 。

都 $GG$ 了（当然我最惨，暴力分居然被卡了，只有 $10$ 分 $QwQ$）。

我们来看一下题目：

题目的阶梯数据真良心！

20分做法

很显然，$n,m \le 5$ ，分明是摆着让我们爆搜，那么直接暴力枚举打那个，处理一下路线的交叉问题就好了。

然而我菜爆了，这个居然打挂了，然后就只剩下 $10$ 分了 $QvQ$。

40分做法

可以加一个剪枝，怎么剪呢？

对于一个炮塔，假设我们之前在其打击范围内已经找到了一个点，该点跟该炮塔的曼哈顿距离是 $x$ ，其权值为 $a$ ,然后现在我们继续 $dfs$ ，发现又找到了一个点也在打击范围内，该点的与该炮的曼哈顿距离是 $y$ ，其权值是 $b$ 。

那么现在我们假设 $xb$ ，那么显然，对于最优的方案，该炮塔肯定不会打 $b$ 权值的点。也就是说，$b$ 权值的点没有 $a$ 权值的点优，因为权值少了，收益没那么大，并且风险(距离)(指容易被打断的风险)增加了。这时我们便可以放弃 $b$ 点，这就是一个小小的剪枝优化。

100分做法

考虑最小割。

对于每一个炮塔，我们将其能打出去的范围的所有点连成一条链，这条链的两端分别连着 $s$ 和 $t$ 。

这个时候的 “割” 就是说你这个炮打到哪里结束。

如下图：

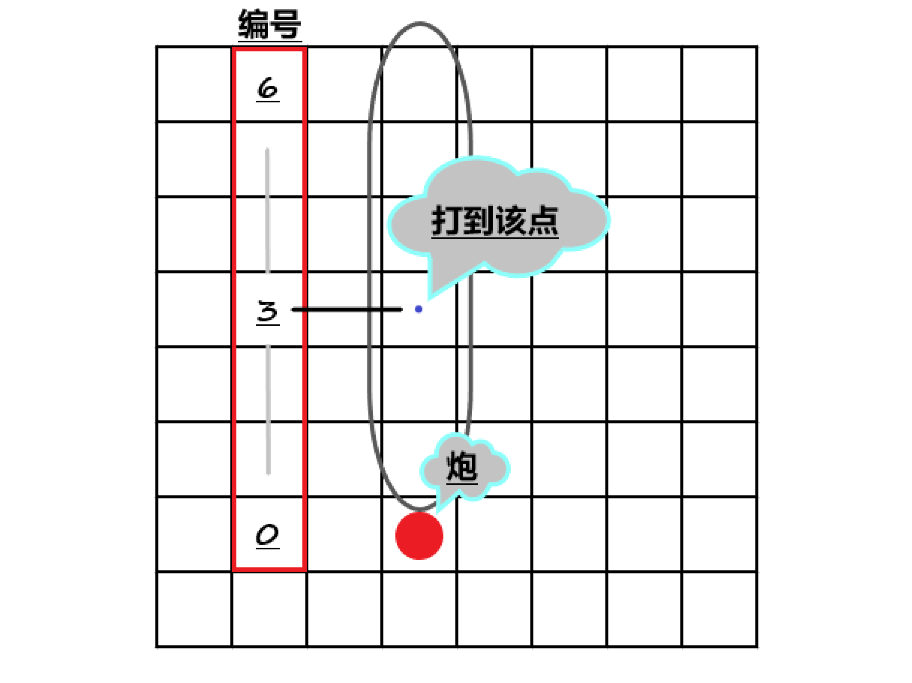
那么网络流的图中，这条链中 $3-4$ 的这条边被切断了。

所以我们每一个炮有一个打到的地方(当然可以不打)，这个时候每一条链都断了，所以图就断了。

但是关系并没有那么简单，假设现在又有一个炮塔，其轨迹跟现在的炮相交了，如果相交的点的编号 $<3$，显然这个红炮是不可以打到小蓝点( $3$ 号点)的，我们该如何表示这种关系呢？

现在所表示的状况：

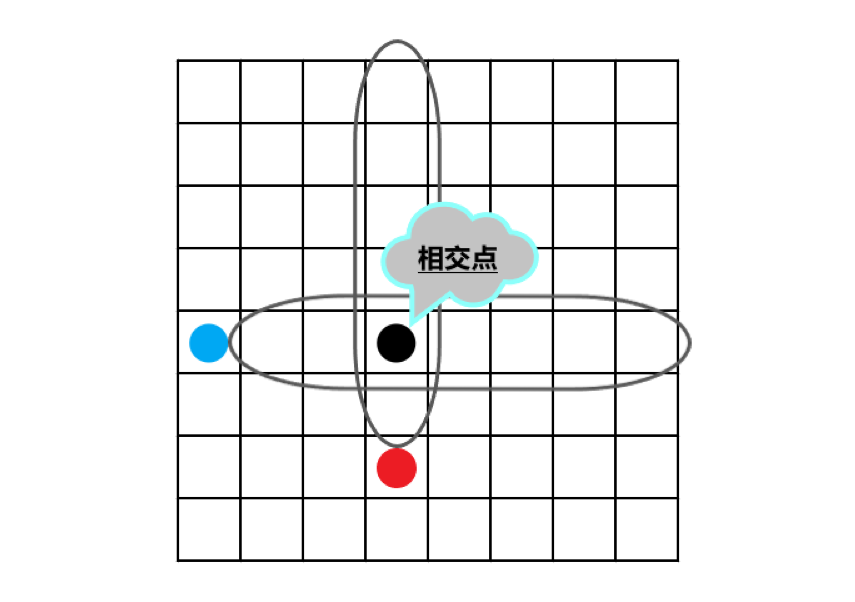
现在的状况就是，相交点上面的点都打不到了(红炮)，相交点右边的点都打不到了(蓝炮)。

但是我们一定要保证 $S$ 到 $T$ 的联通。

那么就可以确定，如果红炮所在的点连接 $S$ ，那么蓝炮就连 $T$，这样才可以使 $S$ 和 $T$ 连通。

然后来解决怎么处理相交点的连边问题。

但是，如果按照上面的 “红炮连 $S$ ，蓝炮连 $T$” 的话，直接这样连不就好了吗？

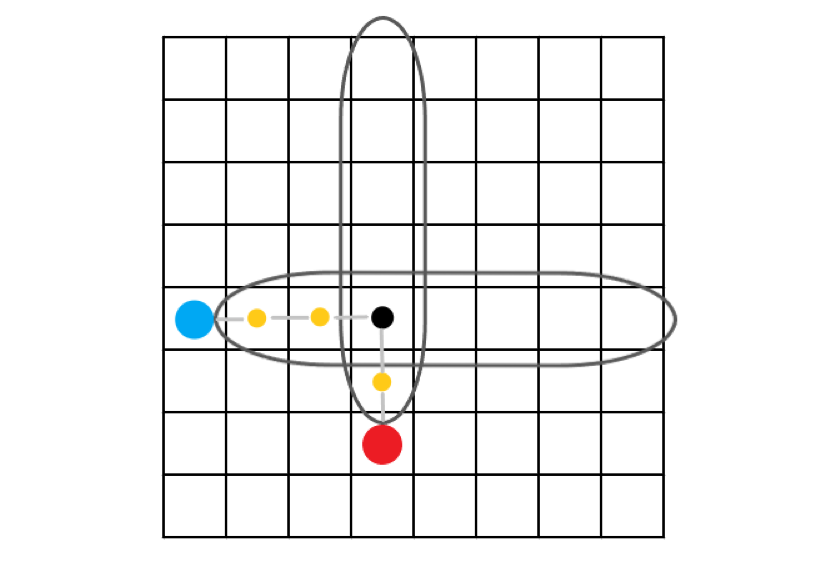
仔细想一想，这其实是布星的，因为我们要保证这个相交点的关系不会被割掉，那么就因该将边值设为 $inf$，但是设哪条边呢？这里所有的边的值都是这个点的权值，我们不可能直接改点的权值吧？

那么很显然，我们将相交点拆成两个点，这两个点中间连有一条边权为 $inf$ 的边，这时无论如何都割不掉这个点了。

最后就是，既然要求最小割，对于如果炮不启动的话边权是 $0$ ，那么就达成了 “最小” 的效果，这是错的。所以我们设一个常量 $T$ ，将每条边的边权都设为 $T-v_i$ 就好。

然后就是板子 $Dinic$。

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<cmath>
#include<queue>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
 
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define id(i,j,type) type*n*m+(i-1)*m+j
 
const int N=5e1+6;
const int inf=1e9+9;
const int dx[4]={-1,1,0,0};
const int dy[4]={0,0,-1,1};
 
int map[N][N],ans,n,m,s,t;
int cnt(1),head[N*N*2],dep[N*N*2];
struct Edge{int nxt,to,val;}G[N*N<<2];
std::queue<int> q;
 
bool bfs(){
    memset(dep,0,sizeof(dep));
    q.push(s);dep[s]=1;
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=head[u];i;i=G[i].nxt){
            int v=G[i].to;
            if(!dep[v]&&G[i].val>0)
                dep[v]=dep[u]+1,q.push(v);
        }
    }return dep[t];
}
int dfs(int u,int flow){
    if(u==t||!flow)return flow;
    int used=0,rlow;
    for(int i=head[u];i;i=G[i].nxt){
        int v=G[i].to;
        if(dep[v]==dep[u]+1&&G[i].val>0){
            used+=(rlow=dfs(v,min(G[i].val,flow-used)));
            G[i].val-=rlow,G[i^1].val+=rlow;
        }
    }if(!used)dep[u]=-1;
    return used;
}
 
int Dinic(){
    int maxflow=0;
    while(bfs())maxflow+=dfs(s,inf);
    return maxflow;
}
 
void add(int u,int v,int w){
    G[++cnt].nxt=head[u],G[cnt].to=v,G[cnt].val=w,head[u]=cnt;
    G[++cnt].nxt=head[v],G[cnt].to=u,G[cnt].val=0,head[v]=cnt;
}
 
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j)
            scanf("%d",&map[i][j]);
    s=0,t=n*m*2+1;
    for(int i=1;i<=n;++i)
        for(int j=1;j<=m;++j){
            if(map[i][j]<0){
                int direction=-map[i][j]-1;
                int x=i,y=j,Mx_val=0;
                while(true){
                    x+=dx[direction],y+=dy[direction];
                    if(x<1||x>n||y<1||y>m)break;
                    Mx_val=max(Mx_val,map[x][y]);
                }ans+=Mx_val;
                if(direction<2)add(s,id(i,j,0),inf);
                else add(id(i,j,1),t,inf);
                x=i,y=j;
                while(true){
                    int tx=x,ty=y;
                    x+=dx[direction],y+=dy[direction];
                    if(x<1||x>n||y<1||y>m)break;
                    if(direction<2)add(id(tx,ty,0),id(x,y,0),Mx_val-max(0,map[tx][ty]));
                    else add(id(x,y,1),id(tx,ty,1),Mx_val-max(0,map[tx][ty]));
                }
            }else add(id(i,j,0),id(i,j,1),inf);
        }
    printf("%d\n",ans-Dinic());
    return 0;
}

为什么之前没想出来呢？

本文标题:【题解】 tower 网络流 bzoj4657

文章作者:Qiuly

发布时间:2019年02月26日 - 00:00

最后更新:2019年03月29日 - 13:52

原始链接:http://qiulyblog.github.io/2019/02/26/[题解]bzoj4657/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。